Written by Imran
on 

গ্রেডিয়েন্ট ডিসেন্ট নিয়ে বোঝাপরা

8 min read

মেশিন লার্নিং নিয়ে যারা কাজ করেন কিংবা শিখছেন তারা অবশ্যই গ্রেডিয়েন্ট ডিসেন্ট ব্যবহার বা এর নাম শুনে থাকবেন। মেশিন লার্নিং এ অন্যতম চ্যালেঞ্জিং পার্ট হল “অপটিমাইজেশন”। আর গ্রেডিয়েন্ট ডিসেন্ট হল মেশিন লার্নিং এ বহুল ব্যবহৃত একটি অপটিমাইজেশন অ্যালগোরিদম। লিনিয়ার রিগ্রেশন,লজিস্টিক রিগ্রেশন, সাপোর্ট ভেক্টর মেশিন, নিউরাল নেটওয়ার্ক সহ আরো অনেক পপুলার মেশিং লার্নিং অ্যালগোরিদমে অপটিমাইজেশনের জন্য গ্রেডিয়েন্ট ডিসেন্ট ব্যবহার করা হয়।

কিন্তু গ্রেডিয়েন্ট ডিসেন্ট নামটা শুনলেই আমাদের চোখে ভাসে নিচের মতো কিছু ঝাঝালো 3D সারফেস প্লটের ছবি। alt text

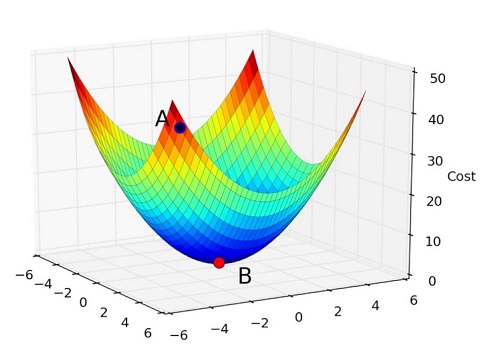
কি ভয়ংকর দেখতে! সাথে আছে এর বিদঘুটে ম্যাথম্যাটিক্যাল ফর্মুলা!

কিন্তু, জিনসটা দেখতে যতোটাই ভয়ংকর, আসলে ততোটাই সহজ, মজার এবং প্র্যাক্টিক্যাল।

চলুন প্রথমেই আমরা এই ঝাঝালো প্লটের ছবি ও গ্রেডিয়েন্ট ডিসেন্ট নিয়ে যতো ভয়ানক অভিজ্ঞতা আছে সব ভুলে যাই। আবার নতুন করে শুরু করি চলুন -

সাধারণ ও বাস্তব ধারণাঃ

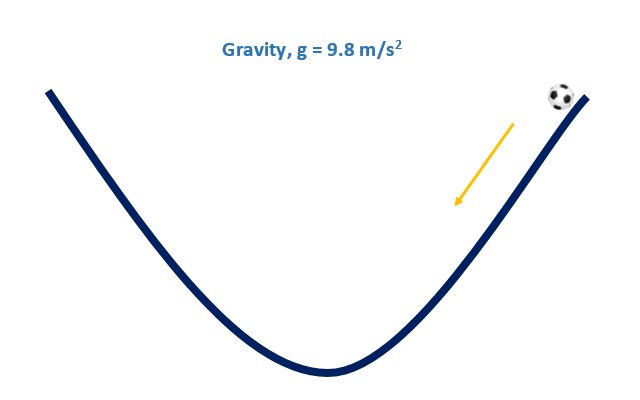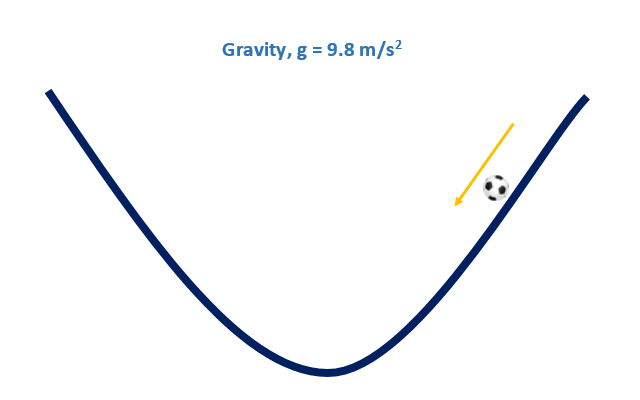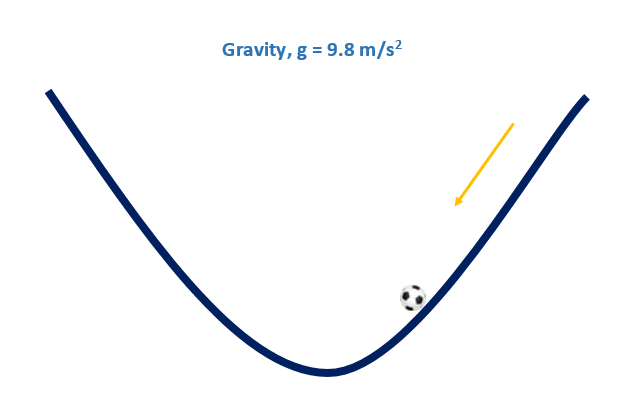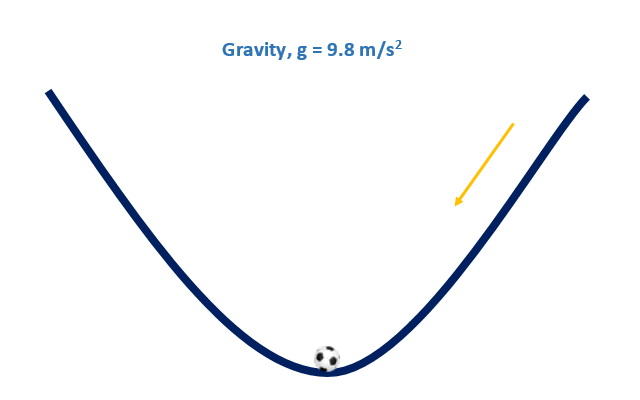
ধরুন, আমরা একটি পুকুরের (গ্রীষ্মের কড়া রোদে পানি শুকিয়ে যাওয়া পুকুর) পাড় থেকে একটি ফুটবল ছেড়ে দিলাম। ঠিক নিচের ছবিটির মত। এখন ঘটনাটা কি ঘটবে?

যেহেতু আমরা জানি যে পৃথিবীতে অভিকর্ষজ ত্বরণ কাজ করে তাই বলটি গড়িয়ে গড়িয়ে পুকুরের ঢালু জায়গার দিকে যেতে থাকবে। যখন পুকুরের সবচেয়ে গভীরে / ঢালু জায়গাটিতে পৌঁছে যাবে তখন বলটি স্থির হয়ে যাবে।

বিষয়টিকে আমরা এভাবেও বলতে পারি যে, বলটি পুকুরের সবচেয়ে মিনিমাম পয়েন্টে যেয়ে থামবে।

alt text

এবার কিছু বাচ্চাকালের ম্যাথেমেটিকাল জিনিস দেখা যাক -

ধরুন, আমাদের একটি ফাংশন দেয়া হলো $f(x) = x^2+5$,

সাথে দেয়া হলো $x$ এর কিছু ভ্যাল্যু, $x = -6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6$

এখন আমাদের কাজ হলো ফাংশনটার সবচেয়ে মিনিমাম ভ্যালুটা বের করা। অর্থাৎ, আমরা এমন একটি ভ্যালু বের করবো যে ভ্যালুটাকে যদি ফাংশনের $x$ হিসেবে ইনপুট দেই তাহলে ফাংশনটা সবচেয়ে মিনিমাম ভ্যালু আউটপুট দিবে।

তাহলে এবার ফাংশনে $x$ এর ভ্যাল্যু গুলো বসিয়ে দেখি আউটপুট হিসেবে কি ভ্যালু পাচ্ছি -

x y = f(x) = x^2+5
-6 41
-5 30
-4 21
-3 14
-2 9
-1 6
0 5
1 6
2 9
3 14
4 21
5 30
6 41

উপরের টেবিল দেখে আমরা সহজেই বুঝতে পারছি যে $x$ এর ভ্যালু $0$ এর জন্য আমারা ফাংশনের সবচেয়ে মিনিমাম ভ্যালু $5$ পাচ্ছি।

এই জিনিসটুকুকে আমরা পাইথন কোডে নিচের মতো করে লিখতে পারি -

import numpy as np

def func(x):
    return x**2+5

x = np.array([-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6])
y = func(x)

print(x)
print(y)
Output:
[-6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6]
[41 30 21 14  9  6  5  6  9 14 21 30 41]

এবার চলুন দেখা যাক ভ্যালু গুলোকে গ্রাফে রিপ্রেজেন্ট করলে কেমন দেখায় -

alt text

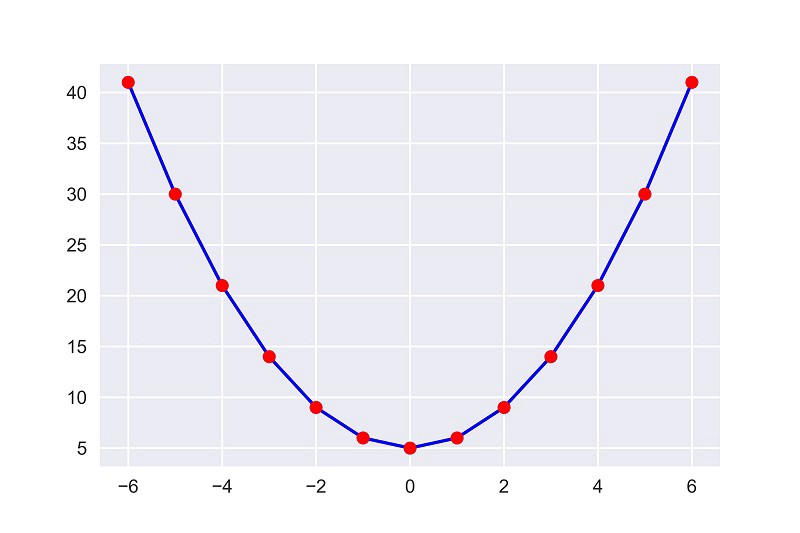
রাফ থেকেও দেখা যাচ্ছে যে $x=0$ এর জন্য আমরা ফাংশনের সবচেয়ে মিনিমাম ভ্যালু $y=5$ পাচ্ছি।

চমৎকার বিষয়টি হলো আমাদের ফাংশনের গ্রাফটি উপরে পুকুরের ছবিটির সাথে মিলে গেছে। এবার শেখা আরো সহজ হয়ে গেলো।

এবার আমরা যদি গ্রাফের উপরের কোন একটা পয়েন্টে ফুটবলটা রাখি, তাহলে কি ঘটনা ঘটবে?

alt text

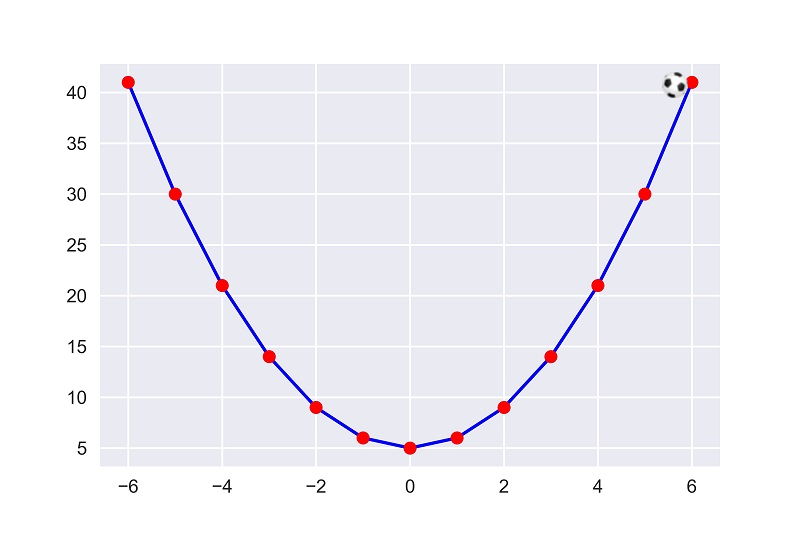
কিছুই ঘটবে না!! বলটা যেখানে রাখা হয়েছ সেখানেই থাকবে। কেননা পৃথিবীতে অভিকর্ষজ ত্বরণ কাজ করে তাই পুকুরের পাড় থেকে বলটি গড়িয়ে ঢালু দিকে নামছিলো কিন্তু আমাদের গ্রাফেতো আর অভিকর্ষজ ত্বরণ কাজ করে না।

তাহলে আমরা কিভাবে বলটাকে গ্রাফের মিনিমাম পয়েন্টে নিয়ে যেতে পারি? এক্ষেত্রে আমাদের ২ টা জিনিস জানা লাগবে -

এবার চলুন গ্রেডিয়েন্ট ডিসেন্ট সম্পর্কে কিছু জেনে নেই। দেখি ইহা খায় না মাথায় দেয়।

গ্রেডিয়েন্ট ডিসেন্টঃ

গ্রেডিয়েন্ট ডিসেন্ট হলো একটি ফার্স্ট অর্ডার আইটেরেটিভ অপ্টিমাইজেশন অ্যালগোরিদম যা কোন একটা ফাংশনের মিনিমাম ভ্যালু খুজে বের করে দেয়।

ফার্স্ট অর্ডার, আইটেরেটিভ এগুলো কি তা একটু পরেই বুঝবো। গ্রেডিয়েন্ট ডিসেন্টে ব্যবহৃত ফর্মুলাঃ

$x_{n+1} = x_n - \gamma \cdot \nabla F(x_n)$

এই ফর্মুলাই আমাদের বলে দিবে বলটি যেখানে আছে সেখান থেকে কোন দিকে কতোটুকু করে আগাতে হবে।

এই ফর্মুলাকে অনেক জায়গায় ভিন্ন নোটেশনেও লেখা হয়। যেমনঃ

এবার ফর্মুলার নোটেশন গুলোর অর্থ বুঝে নেইঃ

$\gamma$ (লার্নিং রেট) তো আমরা নিজেরা সেট করে দিতে পারবো কিন্তু আমাদের মাথা ব্যাথা হলো কিভাবে $x$ এর জন্য $F$ ফাংশনের গ্রেডিয়েন্ট বের করবো, অর্থাৎ কিভাবে $\nabla F(x_n)$ বের করবো।

ফাংশনের গ্রেডিয়েন্ট বের করার নিয়মঃ

কোন একটা ভেরিয়েবলের জন্য কোন ফাংশনের গ্রেডিয়েন্ট হলো সেই ভেরিয়েবলের সাপেক্ষে ফাংশনটিকে একবার ডিফারেনশিয়েট করলে যা পাওয়া যায় তা।

অর্থাৎ, $x$ এর জন্য $F$ এর গ্রেডিয়েন্ট হবে $x$ এর সাপেক্ষে $F$ কে একবার ডিফারেনশিয়েট করলে যা পাবো তা।

ফাংশনটাকে একবার ডিফারেনশিয়েট করলে যা পাবো সেটাকে ওই ফাংশনের ফার্স্ট অর্ডার ডেরিভেটিভ বলে।

তাহলে চলুন দেখি আমরা $x$ এর জন্য $f(x) = x^2+5$ ফাংশনটার গ্রেডিয়েন্ট বের করে ফেলি।

$x_{gradient} = \frac{d}{dx}\cdot f(x)$

$=> x_{gradient} = \frac{d}{dx} (x^2+5)$

$=> x_{gradient} = 2x$

আমরা যদি ক্যালকুলাস ভুলে যাই তাহলেও কোন ব্যাপার না। পাইথনের sympy প্যাকেজ দিয়ে আমরা কোন একটা ফাংশনের ডেরিভেটিভ বের করতে পারবো।

যেমনঃ নিচে দেয়া পাইথন কোডে আমাদের ফাংশনটার ডেরিভেটিভ বের করে দেখানো হয়েছে।

import sympy as sp

x = sp.Symbol('x')

f = x**2 + 5
f_prime = f.diff(x)

print(f_prime)
Output:
2*x

প্রশ্ন হতে পারে যে আমরা এখানে কেনো ফার্স্ট অর্ডার ডেরিভেটিভ নিলাম, ২/৩ বার ডিফারেনশিয়েট করে নেয়া যেতো না?

ফার্স্ট অর্ডার ডেরিভেটিভ নেয়ার কারন হলোঃ

গ্রেডিয়েন্ট এবং ফার্স্ট অর্ডার ডেরিভেটিভ বুঝে থাকলে এবার আসি গ্রেডিয়েন্ট ডিসেন্টকে আইটেরেটিভ কেনো বলা হয়। গ্রেডিয়েন্ট ডিসেন্টের যে ফর্মুলাটা আমরা উপরে দেখলাম সেটি আমাদের পরবর্তী এক স্টেপের জন্য কোন দিকে কতটুকু করে আগাবো তা বলে দেয়। কিন্তু আমাদের তো শুধু এক স্টেপ আগালেই হবে না। আমাদের ততোক্ষণ পর্যন্ত আগাতে হবে যতক্ষণ না আমরা সবচেয়ে মিনিমাম পয়েন্টে পৌছে যাই। তাই আমাদের এই প্রসেসটা একটা লুপের মাধ্যমে নির্দিষ্ট সংখ্যক বার চালাতে হবে।

তাহলে এবার আমরা গ্রেডিয়েন্ট ডিসেন্ট অ্যালগোরিদমটাকে আরেকটু সুন্দর করে গুছিয়ে লিখি -

Repeat until convergence {

       $x_{n+1} = x_n - \gamma \cdot \nabla F(x_n)$

}

এখন গ্রেডিয়েন্ট ডিসেন্টের কোড করার জন্য আমাদের যা যা জানা দরকার সব আমরা জেনে ফেলেছি। এবার ঝটপট কোড লিখে ফেলি চলুন -

gamma = 0.001  
x = 6
iterations = 5000
    
for i in range(0,iterations):
    x_gradient = 2*x
    x1 = x - gamma * x_gradient
    x = x1
        
print("iterations =",iterations,"\nx = ",x)

দেখা যাচ্ছে লুপ $5000$ বার চালালেই আমরা $x$ এর ভ্যালু $0.00026968555624761565$ পেয়ে যাচ্ছি যেটা $0$ এর খুবি কাছাকাছি। এটাকে ইন্টিজারে নিলে আসলে আমরা $0$ ই পাবো। তাহলে পেয়ে গেলাম আমাদের কাংক্ষিত $x$ এর মিনিমাম ভ্যালু যার জন্য আমাদের ফাংশনটি সবচেয়ে মিনিমাম আউটপুট $5$ দিবে।

এবার আমরা গ্রাফে তাকালে দেখবো বলটি ঢালু দিকে গড়িয়ে আগাতে আগতে মিনিমাম পয়েন্ট $0$ তে গিয়ে পৌছাচ্ছে।

alt text

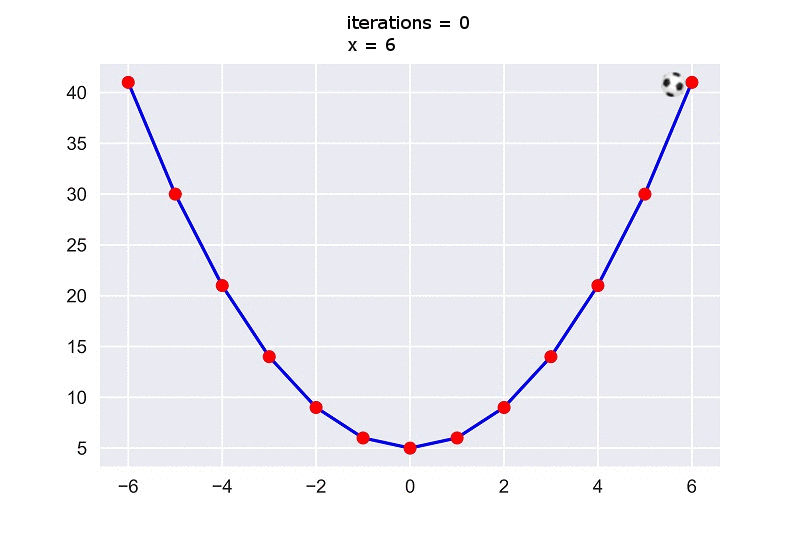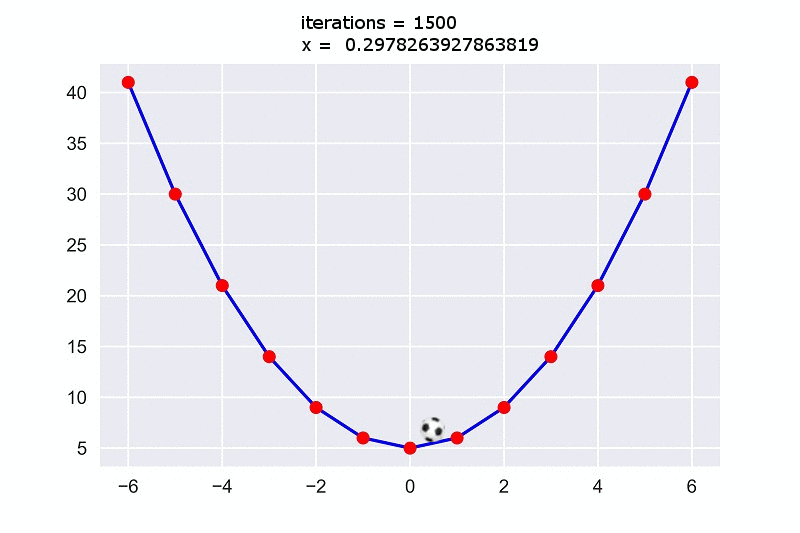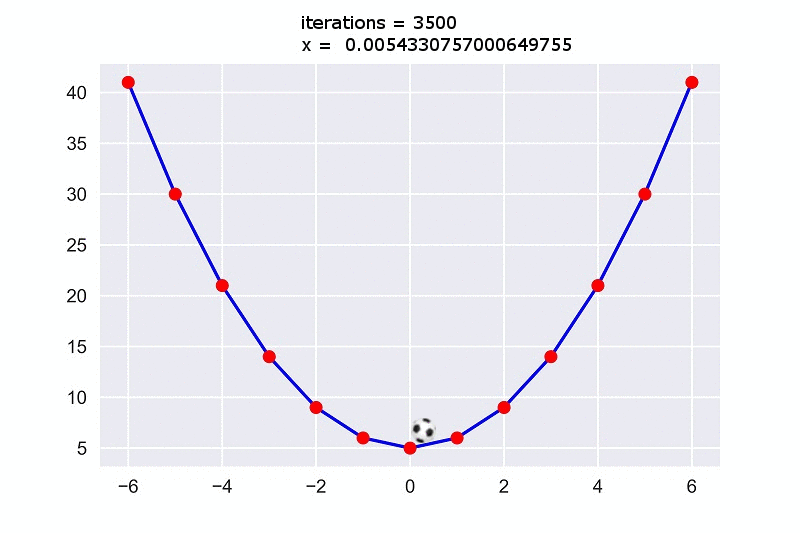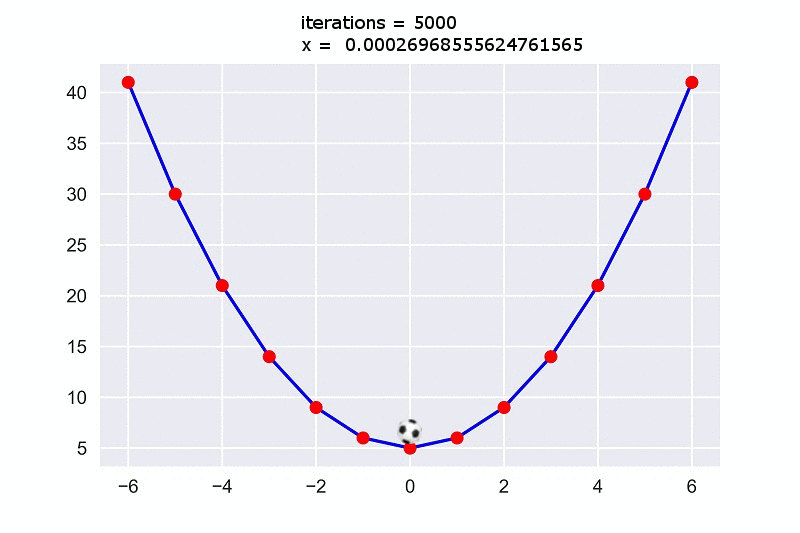
তো এই হলো গ্রেডিয়েন্ট ডিসেন্টে!!

এই লেখাটিতে আমার উদ্দেশ্য ছিলো গ্রেডিয়েন্ট ডিসেন্টের খুবি ব্যাসিক ধারনা দেয়া। তাই আমি ম্যাথেমেটিক্যাল বিষয়গুলো নিয়ে খুব বেশি গভীরে যাইনি।

বোঝার সুবিধার জন্য আমি এখানে খুবি সিম্পল একটি ফাংশন নিয়েছি এবং শুধুমাত্র একটি প্যারামিটার নিয়ে কাজ করেছি। কিন্তু গ্রেডিয়েন্ট ডিসেন্টের আসল অ্যাডভান্টেজ অনুভব করা যাবে যখন আমরা মাল্টিপল প্যারামিটারের জন্য কাজ করবো। পরবর্তী লেখাতে আমরা দেখবো কিভাবে লিনিয়ার রিগ্রেশনের ইরর / কস্ট মিনিমাইজ করতে গ্রেডিয়েন্ট ডিসেন্ট ব্যবহার হয়। সেখানে আমরা মাল্টিপল প্যারামিটার নিয়ে কাজ করবো।

সেই পর্যন্ত আপনারা যতটুকু শিখলেন তা ব্যবহার করে আরো ভিন্ন কিছু ফাংশন নিয়ে কাজ করে দেখুন।

 মেশিন লার্নিং